配位数规则
配位数规则:4→6→8→12
目标:正-负离子相互接触

注意:平面四边形配位和八面体配位是一个条件!
离子、金属半径随配位数增大而增大!
GoldSchmidt半径
随着$r_正$上升,先后出现:仅负离子相切→正负相切(负负不相切)两种情况(和中间的极限情况),根据改变正负离子大小看晶格大小是否改变来推断半径(若晶格改变不大,则改变的那个离子未相切(小))
晶体热力学
晶格能的计算:
定义——固态→气态离子: $$ \ce{M(s) ->M+(g) + X-(g)}\qquad \Delta_{\rm L}H $$ 计算公式: $$ \Delta_{\rm L} H=\frac{N_{\rm A}Mz_Az_B}{d}\left(\frac{e^2}{4\pi\varepsilon_0}\right)\left(1-\frac\rho{d}\right) $$ $M$是马德隆常数,考虑了次级静电作用,而最后一项是修正近距离核间排斥。
简要介绍马德隆常数的计算:
对于NaCl来讲,不难发现: $$ M = \sum_{i,j,k=-\infty}^{\infty}{{\color{red}{(-1)^{i+j+k}}} \over { (i^2 + j^2 + k^2)^{1/2}}} $$ 红色部分巧妙地控制吸引和排斥,注意$i=j=k=0$的情况不在计算之中。
注意到此数列是条件收敛的,一般有两种逼近策略,第一种: $$ \lim_{N \to \infty} \sum_{i^2+j^2+k^2 < N} {{(-1)^{i+j+k}} \over { (i^2 + j^2 + k^2)^{1/2}}} $$ 这种方法相当简单,我们用$C_3(n)$代表将$n$写成三个平方和的方法数量,易得($i^2+j^2+k^2$必定是整数): $$ \sum^\infty_{n=1}\frac{(-1)^nC_3(n)}{\sqrt{n}} $$ 因此我们常常看到如此的序列: $$ M=-6+12/{\sqrt {2}}-8/{\sqrt {3}}+6/2-24/{\sqrt {5}}+\dotsb =-1.74756\dots $$ 然而这个数列是发散的(证明单独成blog),这种方法也是不好。
另一种方法是: $$ \lim_{n \to \infty} \sum_{ -n < i,j,k < n} {{(-1)^{i+j+k}} \over { (i^2 + j^2 + k^2)^{1/2}}} $$ 只有第二种才能给我们需要的结果(十分暴力)。
而Kapustinskii发现,许多结构马德隆常数除以化学式单元中的离子数(总)几乎是个定值→卡公式: $$ \Delta_{\rm L} H=\frac{N_{\rm ion}|z_Az_B|}{d}\left(1-\frac\rho{d}\right)\kappa $$ 这还是太复杂了,引入究极简化——静电参数: $$ \xi=\frac{|z_Az_B|}d $$
判断含氧酸盐的稳定性
看含氧酸盐和氧化物能量的相对变化——大阳离子相对变化小,小阳离子相对变化大。

热力学循环
不少难以直接计算的数据都可以通过热力学循环得到,同样,热力学循环也是解释问题的好帮手。
溶解性:溶解——晶格能 + 阳离子水合能 + 阴离子水合能
离子大小和电荷、离子的软硬、固体的晶体结构以及每个离子的电子结构(构型)都有关。
在阴阳电荷相等时,大大小小规则较为有用:对于小离子盐,异常大的晶格能不能被相对大的水合焓补偿;对于大离子的盐,即使晶格能相对较低,较小的水合焓仍然允许晶格能占主导地位。对于大-小组合,小离子较高的水合焓足够补偿较小的晶格能,因而容易溶解。 $$ \Delta_{\rm L}H\propto\frac1{r_++r_-}\qquad\Delta_{\rm hyd}H\propto\frac1{r_+}+\frac1{r_-} $$ 但上面的讨论忽略了熵的贡献。尽管离子解离时晶格的破坏带来熵增熵,但我们不能不考虑水合产生的氢键变化。盐溶解时水的氢键网络会受到干扰:具有高电荷密度的小阳离子(Li+等)是“结构制造”,在这些阳离子周围形成了更强大的网络(水合壳)→熵减。相比之下,“结构破坏”离子(例如Cs+)具有较低的电荷密度,破坏原有氢键网络后不会形成强大水合壳→熵增。(同样是大大小小:饱和CsI溶液的摩尔浓度是LiF溶液的60倍以上)注意:在大多数时候,$\D H$的影响比$\D S$大
考虑:水合能——Li:-520kJ;Cs:-264kJ;F:-524kJ;I:-308kJ
晶格能——LiF:1024kJ;LiI:748.6kJ;CsF:732kJ;CsI:592kJ
LiF→LiI时,晶格能变化比水合能大(半径和的相对变化大);CsI→CsF时,水合能变化比晶格能更大(半径和的相对变化小)
还要考虑奇怪的结构:
离子对:由溶液中紧密接触的阳离子和阴离子组成,离子对作为一个单元迁移,其净电荷是组成离子电荷的总和:
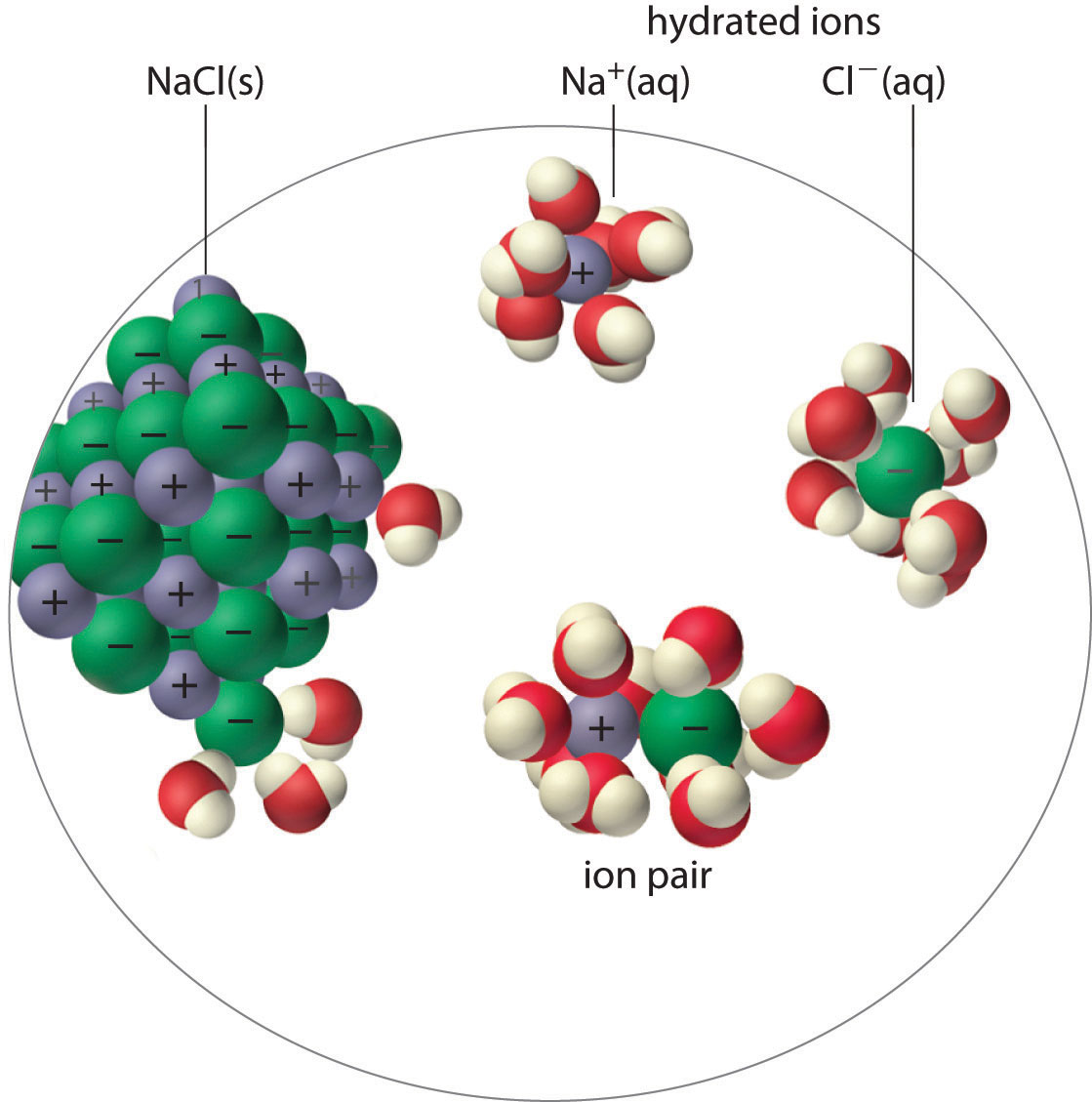
比如,在硫酸钙中,我们需要一个额外的平衡来描述离子对的形成: $$ \ce{CaSO_4(s)<=>Ca^{2+}.SO_4^{2-}(aq)({\text{离子对}}) <=> Ca^{2+}(aq) +{SO_4^{2-}(aq)}} $$ 硫酸钙的测量$K_{\rm sp}$在 25°C 时为$4.93\times10^{-5}$。 如果不考虑离子对,溶解度应为$7.02\times10^{-3}\mathrm M$。事实上,硫酸钙在 25°C 时的实验测量溶解度为$1.6\times10^{-2}\mathrm M$,两倍于它的$K_{\rm sp}$计算值。 产生这种差异的原因是饱和溶液中离子对的浓度几乎与水合离子的浓度一样高。 静电作用对于小的高电荷离子来说更大。,因此,离子对的形成对于含有II价和III价离子的盐(例如$\ce{Ca^{2+}}$和$\ce{La^{3+}}$)来说是最重要的,而对于含有单正阳离子(除了最小的$\ce{Li+}$)的盐来说相对不重要。 因此,我们预计$\ce{CaSO4}$的饱和溶液含有高浓度的离子对,其溶解度将大于$K_{\rm sp}$的预测值。
不完全解离:离子对是离子键未完全破坏;不完全解离则是共价键未完全破坏,溶剂中仍有分子。弱酸 (HA) 的分子(未解离)形式通常非常易溶于水——乙酸与水完全混溶。与硫酸钙一样,我们需要包括一个额外的平衡来描述苯甲酸的溶解度: $$ \ce{C_6H_5CO_2H{(s)}<=>C_6H_5CO_2H{(aq)}<=>C_6H_5CO_2^{−}{(aq)} + H^+{(aq)}} $$ 仅测量离子浓度会严重低估溶液中有机酸的总浓度。 以苯甲酸为例——只有大约 5% 以解离离子的形式存在。
生成配合物:不再赘述。
能带理论
导电好的通常导热也好(电子的移动可以传递能量)。延展性——不活泼的更好
几个名词:满带——充满电子;导带——部分充满;价带——能级最高的填了电子的能带(满带或导带);空带——没有电子;带隙 or 禁带——不能填电子。
s带、p带、d带(比如TiO1)——看那种轨道重叠而成(金属的d和O的p轨道)。
绝缘体——$E_g\ge5\rm eV$;半导体——$E_g<3\rm eV$。费米能级——0K时固体能带中充满电子的最高能级。
解释:温度越高,半导体电阻越小(除金属外都是如此),与金属导电性进行对比:
半导体的导电依赖于热能将电子激发到费米能级以上,形成空穴和电子(二者都可移动并导电)。而金属则不需要这点,影响金属导电性的主要是电子通过金属遇到的阻碍——热振动会加大阻碍(把电子“散射”了)。
半导体对温度的依赖类似于玻尔兹曼表达式,可以认为是: $$ \sigma=\sigma_0\mathrm e^{-E_\mathrm g/2kT} $$ 半金属的情况:(著名的例子有石墨)

无论是Negative型还是Positive型半导体都是在本征半导体的基础上减小带隙:(注意费米能级的位置)

非计量的金属氧化物也分P、N:ZnO、Fe2O3(易被还原)是n型半导体——缺少O原子:电子富余,形成一条小能带(原本是O的lp)——在氧气中加热并冷却导电性下降;Cu2O、FeO、FeS、CuI(易被氧化)是p型半导体——电子缺失,形成空穴——在O2中加热导电性增加;MgO等不易氧化还原(主族)——绝缘体。
PN结2
由于掺杂能级的不同,P型半导体和N型半导体具有不同费米能级:

当PN结形成时,半导体的能带会扭曲——为了拥有相同的费米能级:

扩散运动:随机热运动,电子:N→P;空穴:P→N
电子与空穴复合,导致扩散到对面的多数载流子都耗尽了,结区只剩下不可移动的带电离子,失去了电中性变为带电,形成了耗尽层。耗尽区形成的内建电势的方向与扩散相反,阻碍进一步扩散。
漂移运动:在外加电场(内建电势)下运动
当我们外加电压使PN结正偏时,外加电场与内建电场方向相反,当外压足够大时,电子可以由N至P运动(其实和扩散运动方向一致),称PN结导通。
当PN结反偏时,耗尽层会变厚。并且随反向偏置电压的增加,耗尽层的厚度增加,扩散过PN结的势垒增大,电阻变大,宏观看二极管成为绝缘体。除了正向偏压导通之外,PN结还会被反向击穿:
- 如果反向电压过大,PN结中的载流子会拥有很大的动能,足以和中性粒子碰撞使中性粒子分离出价电子而产生空穴-电子对。这样会导致PN结反向电流的急剧增大,发生PN结的击穿,因为被弹出的价电子又可能和其他中性粒子碰撞产生链式反应,类似于雪崩,这样的反向击穿方式成为雪崩击穿。掺杂浓度越低所需电场越强。
- 当掺杂浓度非常高时,在PN结两端加入弱电场就会使中性粒子中的价电子脱离原子的束缚,从而成为载流子,导致PN结的击穿。这样的击穿被称作齐纳击穿。
其他二极管
光敏开关:在反偏时,光照可能使电子激发到导带上,使电子可以流动(变相击穿?)

太阳能电池板:光敏开关作为电源。

LED:正偏PN结可以逆转太阳能电池板的过程,当两种载流子在耗尽层合体时,如果产生的能量变化幅度合适,它可以作为可见光释放。
量子点
连续的能带是大量粒子时的近似,若半导体足够小(10nm),它会显示出离散的能级。让量子点的载流子发生变化需要更多能量,从而调整颜色。

注意到随着纳米晶体尺寸的增加,带隙变得更小,并且发射最大值移动到更高的波长(更低能量)。3
超导——原理
I型,如Nb-Ti 合金。具有迈斯纳效应——在冷却到临界温度 Tc 以下时会排出所有磁通量。 在磁场超过临界值Hc后施加的磁场会破坏超导性。(突变)

II型超导体更为复杂:排斥→部分排斥→正常(大多高温超导体)

一个常见的演示是将一小块超导材料冷却到其临界温度以下,然后在其上方放置一个小磁铁。 磁铁悬浮在超导体上方固定位置。
悬浮演示仅适用于 II 型超导体,因为需要进入超导体的磁场线来阻止横向运动,并让斥力和引力的平衡——磁通钉扎。

磁性

名词:磁化率χ:磁化强度M与磁场强度H之比
铁磁性:在Curie温度以下自旋锁定平行,具有极大的极化率。一般d轨道(较少:f)含有未成对电子会有铁磁性。相互作用——使得自旋平行但没有成共价键。得到滞后曲线→达到某个状态后不易改变,无法原路返回。分软硬:硬(蓝色)——在外加磁场下难变化→永磁体;软(红色)——容易变化→变压器。

反铁磁性:在Neel温度下磁化率急剧下降,自旋被锁定在反平行,常见原因:超交换(大π键)

超交换——180°→反铁磁性;90°→铁磁性
亚铁磁性:两种不同粒子的电子平行or反平行(无法完全抵消),还是有弱的铁磁性。如Fe3O4中两种Fe。
总结如下:
| 磁性行为 | 磁化率随温度变化 | 场依赖性 |
|---|---|---|
| 抗磁性(无单电子) | 无 | 否 |
| 顺磁性(a) | 下降 | 否 |
| 铁磁性(b) | 下降 | 是 |
| 反铁磁性(c) | 增加(Neel以下) | (是) |



