副族之间的键

引入 #

在研究主族元素化学时，等电子原理是非常好用的手段（如BN-C）等等，但等电子原理在处理副族时遇到了困难——副族金属倾向于18电子而非8电子。怎么办呢？一个巧妙的办法是作差——看还缺几个电子来达到满壳层。

已经满壳层（稀有气体或满足18电子）的物种十分稳定，不需多说。

缺一个电子满壳层（卤素和17电子物种）有不少相似之处：尤其是Co(CO)₄。

缺两个电子：例：S和Fe(CO)₄

当然，作差的类比也会遇到硬茬——不符合八隅律的超价化合物（IF₇、XeF₄还没找到金属有机类似物）；对金属而言，当配体不如CO时，18电子规则可能就没有那么好用了，相似性也会大大减小。

等瓣相似 #

当两个分子片段等瓣相似时，它们前沿轨道的数量、对称性、能量、形状以及其中的电子数是相似的。¹

我们可以就用杂化轨道理论推导（中间的电子相当于非键）²：

不要把等瓣相似和开头的作差法混为一谈，虽然二者不少时候都能得到相同结果（尝试：Cr(CO)₅、Fe(CO)₅）。简化思考的方法——考虑电子数（作差）、可成键轨道数³（一般六个d²sp³）。

我们可以在两端增减电子⁴：

同样，可以将等瓣相似拓展到四边形配位，但相应的d电子数要加2（一个成键轨道不参与杂化，变为非键）

更多——三角双锥、四面体……）

特别注意：（下面的非键轨道只写d轨道）

我们把一个个片段全部等效成CH₃（也就是H）、CH₂、CH、C，也可以再用等电子原理推广成P、S等其他原子找熟面孔，接下来的推断我相信没有人不会。

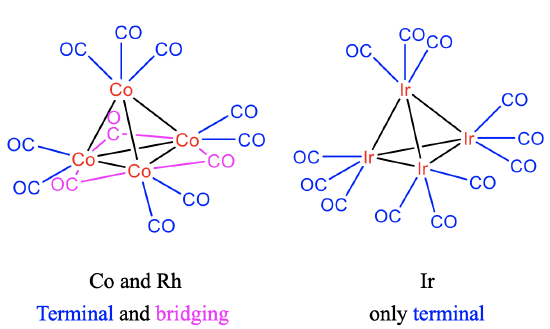
但等瓣相似也不是绝对的，尤其是针对第一过渡系原子的多聚物，常有意想不到的桥破坏对称性（其实成不成桥对18电子规则等没有影响）

例：P5^-——Cp^-

例：Ph₃PAu——CH₃——H（自己画画轨道）

Co(CO)₄(AuPPh₃)等不用多说，甚至有Ti(CO)₆(AuPEt₃)^-（Ti七配位）

金属-金属键 #

同样可以认为是等瓣相似的结果（可惜没有δ键，某人朝思暮想的碳碳四键并不存在）

画出MO图，发现——Re₂Cl₈^n-中Re-Re五重键可能不？No，那是因为四个配体与一个形成δ键的轨道作用从而使其能量发生改变⁵（这也是为啥大多数“5重键”物种配位数极低）正因如此，四重键才是强制重叠的（配体方向的轨道因为与配体作用而不能再成δ键）。

四重键与三重键（特别是去除δ*的电子）键长没啥区别——1.键级上升，有缩短趋势；2.库伦排斥上升，有变长趋势；3.有效核电荷上升，d轨道收缩，π键（δ太弱不考虑）成键变弱。

五重键——低配位数（对d轨道能量影响较少不妨碍成δ键）；大（动力学保护）